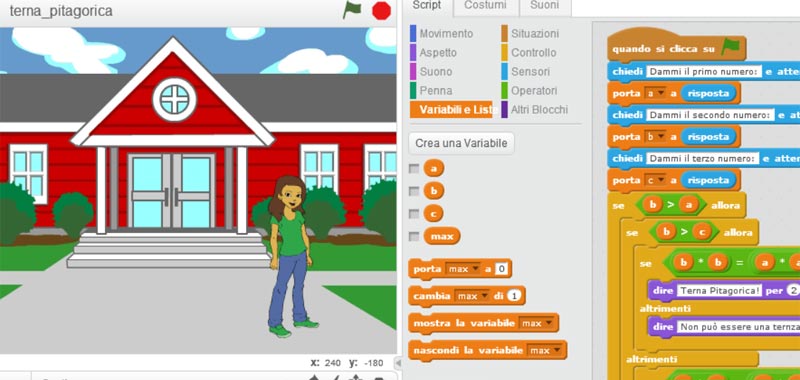
Realizziamo oggi un semplice programma sulla terna pitagorica utilizzando Scratch.
Il termine deriva da Pitagora. Infatti la terna pitagorica è l’aspetto aritmetico, del ben noto teorema geometrico di Pitagora, di cui ricordiamo l’enunciato:
In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Quindi, dal punto di vista aritmetico, se tre numeri interi a, b e c verificano la relazione a2 + b2 = c2, allora si dice che formano una terna pitagorica.
Esistono dunque infinite terne con numeri interi che soddisfano questa condizione, come ad esempio: 3, 4 e 5 oppure 5, 12 e 13 e così via.
Terna pitagorica con Scratch
Si realizzi dunque un programma che legga in input tre valori (a, b e c) e determini se questi numeri possono formare una terna pitagorica, utilizzando la programmazione a blocchi con Scratch.
Banner Pubblicitario
Innanzitutto scegliamo uno sfondo e uno sprite qualunque.
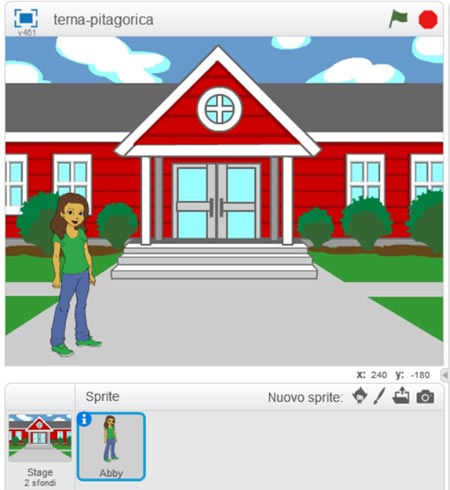
Dopo creiamo tre variabili: a, b e c.
Chiediamo di inserire il primo cateto (a), dopo il secondo cateto (b) ed infine l’ipotenusa (c).
Quindi verifichiamo che la proprietà descritta sopra sia soddisfatta.
Ecco quindi il codice completo:
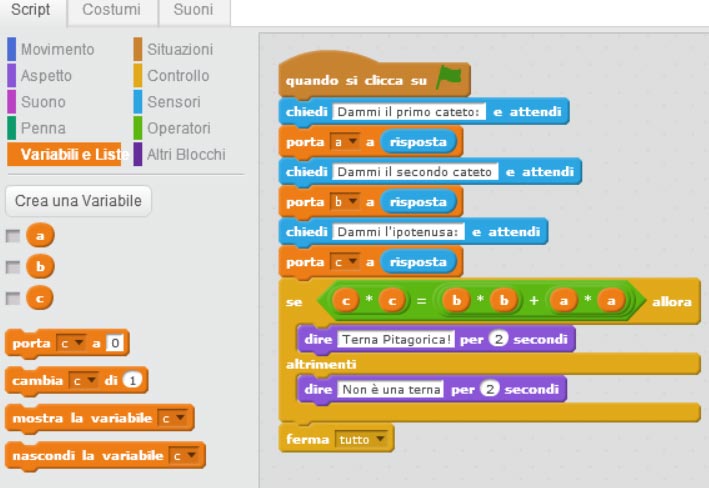
In questo modo verifichiamo che il triangolo è rettangolo dal punto di vista geometrico e che i tre numeri formano una terna pitagorica dal punto di vista aritmetico.
Bene, ma se non volessimo dare importanza all’ordine di inserimento dei dati?
Banner pubblicitario
In questo caso allora occorre, prima di applicare la formula, calcolare il valore massimo tra i tre valori inseriti in input.
Quindi controlliamo innanzitutto se b è maggiore di a e se è vero allora:
– controllo se b è maggiore di c e:
– se vero allora si deve verificare che: a2 + c2= b2;
– se invece è falso si deve verificare che: a2 + b2 = c2.
– invece se b maggiore di a è falso allora controllo se a è maggiore di c:
– se vero allora si deve verificare che: c2 + b2= a2;
– se falso invece si deve verificare che: a2 + b2 = c2.
Ecco dunque la seconda soluzione dell’algoritmo sulla terna pitagorica con scratch.
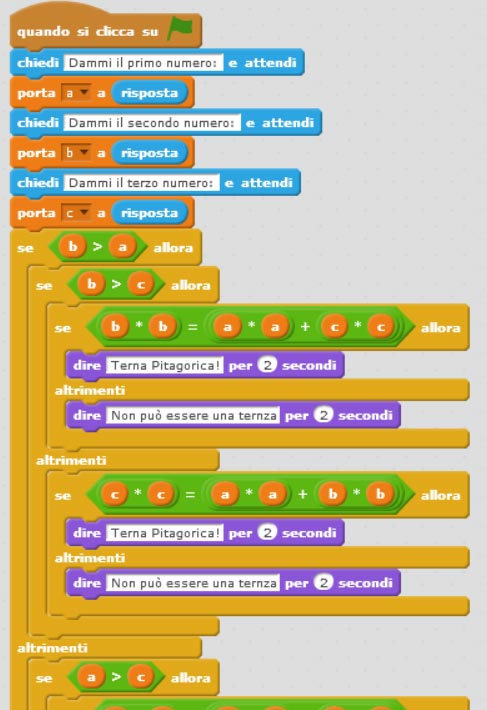
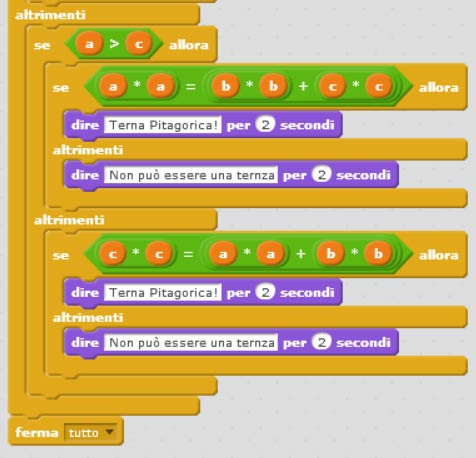
Chiaramente la soluzione proposta è solo uno dei possibili metodi per realizzare l’algoritmo sulla terna pitagorica con Scratch.
Alcuni link utili
Divisori di un numero con scratch
Multipli di un numero con scratch
Quoziente potenze stessa base con scratch
Operazioni matematiche con scratch
Commenti recenti