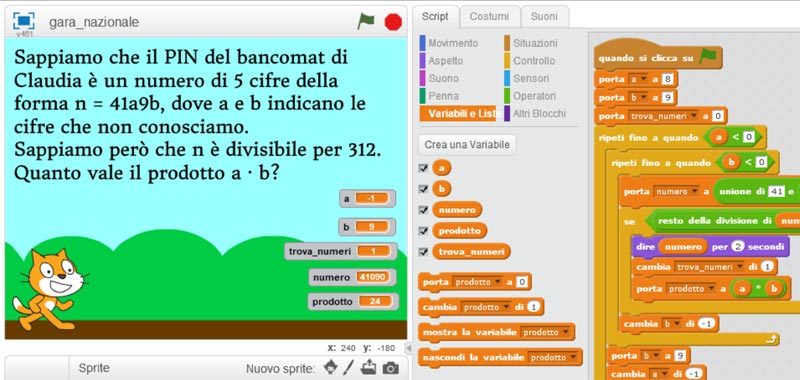
In quest’articolo affronteremo un quesito delle olimpiadi di matematica con scratch.
Sappiamo che il PIN del bancomat di Claudia è un numero di 5 cifre della forma n = 41a9b, dove a e b indicano le cifre che non conosciamo. Sappiamo però che n è divisibile per 312. Quanto vale il prodotto a · b?
Ragioniamo sul numero da trovare.
Se a e b fossero uguali a 9, cioè la più alta combinazione possibile, il nostro numero sarebbe 41999.
Questo numero diviso 312 mi dà 134 con resto 191 e 134 x 312=41808.
Quindi non può essere 134 perchè deve essere soddisfatta la seguente condizione 41a9b. Dunque il numero da trovare è minore di 134.
Se invece a e b fossero uguali a zero, ovvero la più piccola combinazione possibile, il nostro numero sarebbe 41090. Se lo dividiamo per 312 avremo:
41090/312= 131 con resto 7 e 131 x 312 = 40872
Il numero è comunque troppo piccolo, quindi possiamo scartare 131.
Per i ragionamenti appena fatti gli unici divisori possono dunque essere 132 e 133.
Facendo le operazioni possiamo escludere 132, in quanto:
132 x 312 = 41184 e chiaramente non può essere perchè deve essere soddisfatta la seguente condizione 41a9b.
Perciò l’unico divisore è 133, infatti se lo moltiplichiamo per 312 mi darà il numero 41496.
133 x 312= 41496 e la condizione 41a9b è soddisfatta.
Quindi a=4 e b=6
Dunque il prodotto di a per b è 24.
Proviamo adesso a risolverlo con un algoritmo.
Algoritmo su un quesito delle olimpiadi di matematica con scratch
Consideriamo il nostro numero 41a9b, dove a e b sono due variabili che possono variare ognuna da 0 a 9.
Queste sono le variabili che servono:

Scelgo uno sfondo e uno sprite qualunque e inserisco il testo, del problema delle olimpiadi di matematica, direttamente nello sfondo.
Cliccando sullo stage compaiono gli strumenti per personalizzare gli sfondi:
Quindi consideriamo due cicli annidati per provare tutte le possibili combinazioni finchè non troverà il numero cercato.
Ecco lo script completo che ripete partendo da a e b uguali a 9 tutte le possibili combinazioni.In sostanza proverà dapprima il numero 41999 poi 41998,..,41997, …,41990,41899… ecc… fino a trovare il numero divisibile per 312.
Per verificare se il numero è divisibile per 312 si considera l’operatore presente in scratch: resto della divisione e lo si confronta con zero.
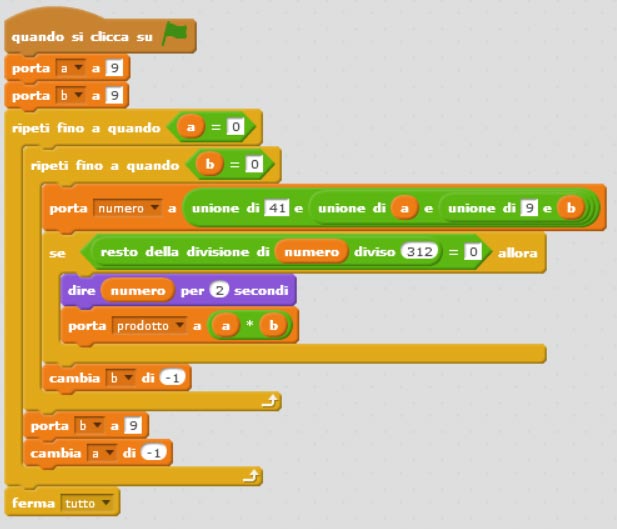
Potremmo migliorare l’algoritmo e farlo fermare non appena trova il divisore. Basta spostare il ferma tutto sotto l’istruzione prodotto.
Oppure creare una variabile di controllo.
Questo è solo un quesito delle olimpiadi di matematica con scratch, ve ne proporrò degli altri.
Alcuni link utili:
Figure equivalenti con scratch
Riconoscere gli angoli con scratch
Giochi matematici autunno 2018
Esempi di giochi matematici Bocconi
Gioco della tabellina con scratch
Gioco indovina numero con scratch
Equazioni di primo grado con scratch
Disegnare poligoni regolari con scratch
La successione di Fibonacci in Scratch
Massimo fra tre numeri in Scratch
Minimo tra 3 numeri in Scratch