Un numero si dice perfetto quando la somma dei suoi divisori propri è uguale al numero stesso. Per divisori propri si intende tutti i divisori tranne il numero stesso.
Alcuni esempi di numeri perfetti sono 6, 28, 496, 8128, ecc…
Infatti se consideriamo il numero 6 i divisori propri sono 1, 2 e 3. La somma di questi divisori è proprio 6.
Se consideriamo il numero 28 la somma dei divisori è 1+2+4+7+14=28.
Quindi in definitiva per risolvere l’algoritmo con Scratch basta trovare tutti i divisori di un numero e sommarli.
Numero perfetto con Scratch
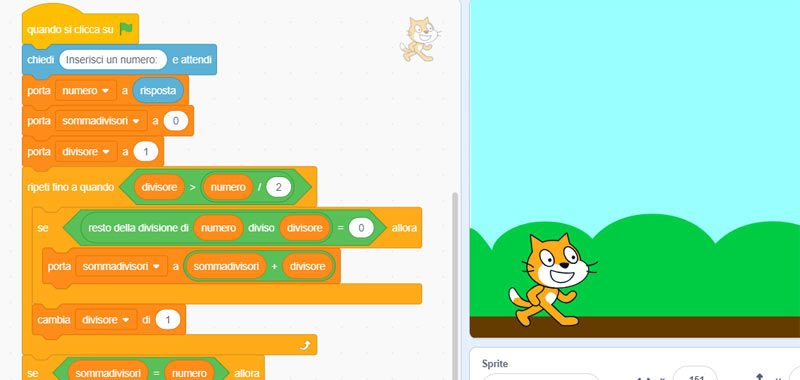
Ecco il funzionamento dell’algoritmo.
Spieghiamo l’algoritmo passo passo.
Innanzitutto scegliete uno sfondo a piacere. Dopo chiediamo all’utente di inserire un numero e lo memorizziamo in una variabile.

Adesso impostiamo la variabile divisore ad 1, cioè cominciamo a dividere per 1 il numero preso in input. Dopo impostiamo la variabile sommadivisori a 0.

Quindi inseriamo il ciclo ripeti fino a quando inserendo la condizione divisore>numero/2. Cioè continueremo a dividere il numero finché il divisore sarà uguale alla metà del numero. Infatti, dato che dobbiamo escludere come divisore il numero stesso e dato che è scontato che dividere un numero per valori maggiori della sua metà dà resto diverso da 0, possiamo fermarci alla sua metà.
Ad esempio se il numero preso in input è 6, il divisore si ferma a 3.
Quindi ecco il prossimo passaggio:

Adesso dobbiamo controllare se il resto della divisione di numero diviso divisore è uguale a zero. Se questa condizione è vera il divisore si somma alla variabile sommadivisori.
In ogni caso si incrementa il divisore di 1.
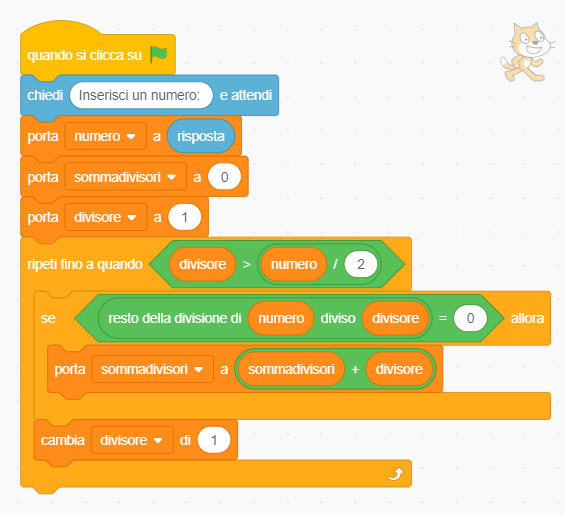
Quindi rimane da controllare se il numero è uguale a sommadivisori, se questa proprietà è verificata allora il numero è perfetto, altrimenti non lo è.
Ecco dunque l’algoritmo finito:

Alcuni link utili
Massimo fra tre numeri in Scratch
Minimo tra 3 numeri in Scratch
Esempio di successione di Fibonacci con Algobuild
La successione di Fibonacci in C++