Un numero di Harshad è un numero naturale divisibile per la somma delle sue cifre.
I numeri di Harshad minori o uguali a 100 sono: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72, 80, 81, 84, 90, 100.
Algoritmo sul numero di Harshad
Dato un numero in input, determinare se è un numero di Harshad.
La risoluzione di questo algoritmo consiste nel sommare le cifre e vedere se il numero di partenza è divisibile per la somma.
Quindi come primo passo dobbiamo studiare il modo per sommare le cifre e lo facciamo considerando i resti delle divisioni del numero per 10.
Facciamo un esempio prendendo in considerazione il numero 24.
24 / 10 = 2 resto 4 continuiamo a dividere
2 / 10 = 0 resto 2
Se facciamo la somma dei resti otteniamo la somma delle cifre, cioè 6.
Dopo controlliamo se 24 / 6 dà resto 0 e se ciò è vero allora il numero è di Harshad.
Migliora le tue capacità di programmazione Python seguendo i nostri corsi in diretta!
Realizziamo adesso il nostro algoritmo in python. Quindi prendiamo una variabile di nome s dove vado a sommare i resti delle divisioni.
Si rende necessario copiare il valore di n in un’altra variabile, ad esempio h, perché il numero n viene diviso per trovare le cifre da sommare.
Ecco quindi una possibile soluzione. In questo caso come potete notare è preferibile usare il while.
n = int(input('Numero: '))
s, h = 0, n
while n > 0:
s += n % 10
n = n // 10
if(h % s == 0):
print('Numero di Harshad')
else:
print('Non è un numero di Harshad')Secondo algoritmo
Trovare i numeri di Harshad da 1 a 100.
In questo caso abbiamo bisogno di due cicli. Uno esterno che utilizza un contatore ed uno interno che divide finché non si verifica la condizione specifica.
Quindi chiaramente per realizzare il ciclo esterno occorre un ciclo for, mentre per quello interno conviene utilizzare il while.
Utilizziamo l’indice i che va da 1 a 100, quindi dobbiamo indicare nel range l’intervallo (1,101)
Per ogni i si controlla poi se vale la proprietà di Harshad, dividendo per la somma delle cifre, come abbiamo fatto nell’algoritmo precedente.
Se tale condizione è verificata alla fine del ciclo interno stamperemo il numero, altrimenti non facciamo nulla.
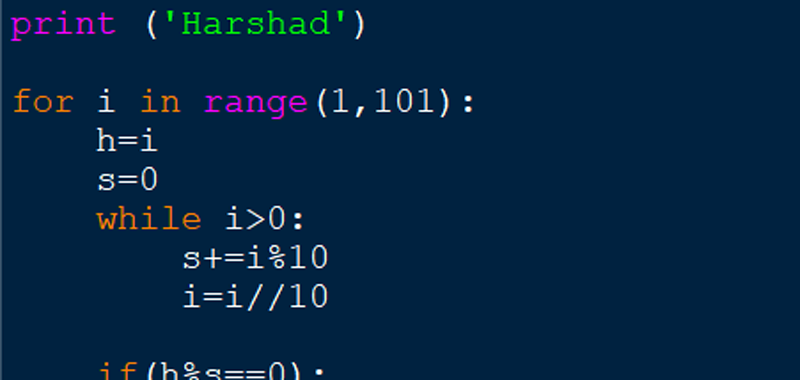
Ecco dunque una possibile soluzione all’algoritmo proposto:
for i in range(1,101):
h = i
s = 0
while i > 0:
s += i % 10
i = i // 10
if(h % s == 0):
print(h, end=' ')Alcuni link utili
Indice tutorial sul linguaggio python
1 – Introduzione al linguaggio python
3 – Operatori aritmetici e di assegnazione in python
8 – Errori in python
9 – Script python
10 – Scambio di variabili in python
11 – Libreria math