Numeri amicabili in Python, trovare i divisori di un numero

In questa lezione realizzeremo un programma sui numeri amicabili in Python, al fine di esercitarci con le strutture iterative.

Ricordiamo che due numeri si dicono amicabili se la somma dei divisori propri di uno, escluso però il numero stesso, è uguale all’altro numero e viceversa.

Ad esempio i numeri 220 e 284 sono amicabili.

Infatti i divisori di 220 sono 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110. La loro somma mi dà 284.

Allo stesso modo troviamo i divisori di 284: 1, 2, 4, 71, 142 la cui somma fa 220.

Quindi i numeri sono amicabili.

L’algoritmo risolutivo consiste dunque nel trovare tutti i divisori del primo numero, escluso il numero stesso, sommarli e confrontarli con l’altro numero. Allo stesso modo con il secondo numero.

Esplora il mondo della programmazione con il libro “50 Algoritmi per imparare Python” e libera la tua creatività!

Scopri tutto il potenziale di Python con la “Guida Completa a Python – Dalle Basi alla Gestione dei Moduli e dei File”!

Acquistalo su Amazon

Numeri amicabili in Python

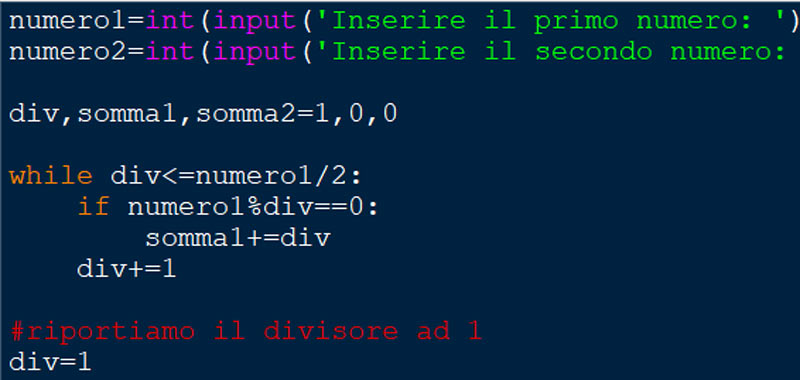
Quindi innanzitutto prendiamo in input i due numeri interi e li memorizziamo in due variabili numero1 e numero2. Dopo inizializziamo le variabili div, somma1 e somma2.

La variabile div rappresenta il divisore e viene inizializzata ad 1 all’inizio e dopo il primo while, perché ci servirà per l’altro numero. In alternativa si poteva utilizzare un’altra variabile.

Dopo con il ciclo while troviamo tutti i divisori del numero1 e li sommiamo nella variabile somma1. Lo stesso per l’altro numero per cui sommiamo i divisori nella variabile somma2.

Infine compariamo somma1 con numero2 e somma2 con numero1. Se entrambe le uguaglianze sono verificate allora i numeri sono amicabili, altrimenti non lo sono.

Ecco dunque il codice completo dell’algoritmo sui numeri amicabili in Python:

numero1 = int(input('Inserire il primo numero: '))
numero2 = int(input('Inserire il secondo numero: '))

div, somma1, somma2 = 1, 0, 0

while div <= numero1 / 2:
    if numero1 % div == 0:
        somma1 += div
    div += 1

div = 1  # Riportiamo il divisore ad 1

while div <= numero2 / 2:
    if numero2 % div == 0:
        somma2 += div
    div += 1

if somma1 == numero2 and somma2 == numero1:
    print('I numeri sono amicabili!')
else:
    print('I numeri non sono amicabili!')

La stessa soluzione si può ottenere con i ciclo for:

numero1 = int(input('Inserire il primo numero: '))
numero2 = int(input('Inserire il secondo numero: '))

somma_divisori_1 = 0
somma_divisori_2 = 0

# Calcolo la somma dei divisori propri per il primo numero
for div1 in range(1, numero1 // 2 + 1):
    if numero1 % div1 == 0:
        somma_divisori_1 += div1

# Calcolo la somma dei divisori propri per il secondo numero
for div2 in range(1, numero2 // 2 + 1):
    if numero2 % div2 == 0:
        somma_divisori_2 += div2

# Verifico se i numeri sono amicabili
if somma_divisori_1 == numero2 and somma_divisori_2 == numero1:
    print('I numeri sono amicabili!')
else:
    print('I numeri non sono amicabili!')

Potremmo aggiungere un controllo, perché in effetti è inutile trovare tutti i divisori del secondo numero, se somma1 è diverso da numero2.

Quindi sarebbe opportuno trovare i divisori del secondo numero solo se la condizione somma1 uguale a numero2 è soddisfatta.

Lo stesso algoritmo lo abbiamo realizzato con algobuild: numeri amicabili con Algobuild.

Ottimizzazioni numeri amicabili in Python

Possiamo ottimizzare l’algoritmo precedente utilizzandoo le “generator expressions” per calcolare la somma dei divisori propri di ciascun numero, rendendo il codice più compatto. Sostituiamo i cicli for con l’utilizzo della funzione sum, che è più efficiente.

Migliora le tue capacità di programmazione Python seguendo i nostri corsi in diretta!

Ecco di seguito il codice ottimizzato:

numero1 = int(input('Inserire il primo numero: '))
numero2 = int(input('Inserire il secondo numero: '))

# Calcolo la somma dei divisori propri per il primo numero
somma_divisori_1 = sum(div1 for div1 in range(1, numero1 // 2 + 1) if numero1 % div1 == 0)

# Calcolo la somma dei divisori propri per il secondo numero
somma_divisori_2 = sum(div2 for div2 in range(1, numero2 // 2 + 1) if numero2 % div2 == 0)

# Verifico se i numeri sono amicabili
if somma_divisori_1 == numero2 and somma_divisori_2 == numero1:
    print('I numeri sono amicabili!')
else:
    print('I numeri non sono amicabili!')

Questa versione ottimizzata riduce il codice e migliora l’efficienza usando espressioni generator e la funzione sum() per il calcolo delle somme dei divisori, evitando cicli for espliciti.

Conclusioni

In questa lezione abbiamo esaminato come implementare un programma in Python per verificare se due numeri sono amicabili, ovvero se la somma dei divisori propri di ciascun numero corrisponde all’altro numero. Abbiamo analizzato diversi approcci per implementare questo programma, ciascuno con i propri vantaggi e considerazioni.

Il primo approccio utilizzava cicli while e variabili per controllare i divisori dei numeri inseriti. Successivamente, ho realizzato la stessa soluzione, sostituendo i cicli while con cicli for, eliminando le variabili non necessarie.

Successivamente, ho proposto una versione ottimizzata utilizzando le espressioni generator e la funzione sum() per ridurre ulteriormente la complessità del codice.

Chiaramente questi sono solo dei possibili modi per implementare l’algoritmo sui numeri amicabili in Python. Ci sono molteplici modi per implementare l’algoritmo per verificare i numeri amicabili in Python, e ognuno può avere vantaggi e svantaggi a seconda del contesto e delle preferenze personali.

Miglioramenti e ottimizzazioni

Ecco alcuni punti da prendere in considerazione:

Approccio Iterativo vs. Approccio Funzionale: Nel nostro esempio, abbiamo utilizzato un approccio iterativo con cicli while e for, ma è possibile implementare lo stesso algoritmo utilizzando un approccio più funzionale con le funzioni built-in di Python come filter() e sum(). Questo potrebbe rendere il codice più compatto e leggibile per alcuni programmatori.
Ottimizzazione degli Algoritmi: Esistono diverse strategie per ottimizzare l’algoritmo per verificare i numeri amicabili. Ad esempio, è possibile limitare il range dei divisori da controllare, in quanto i divisori propri di un numero non possono essere mai superiori alla sua metà. Questo può ridurre il numero di iterazioni e rendere l’algoritmo più efficiente, soprattutto per numeri grandi.
Uso di Funzioni: Abbiamo introdotto una versione che utilizzava una funzione separata per calcolare la somma dei divisori di un numero. Questo rende il codice più modulare e favorisce il riutilizzo del codice. Tuttavia, in alcuni casi, l’uso di funzioni può aggiungere complessità non necessaria, quindi è importante valutare se è realmente vantaggioso.
Gestione dei Numeri Negativi o Nulli: Nel nostro esempio, abbiamo supposto che gli utenti inseriscano numeri positivi, ma potrebbe essere necessario gestire anche numeri negativi o nulli, a seconda dei requisiti dell’applicazione.

È importante scegliere l’approccio che meglio si adatta alle esigenze specifiche del progetto, tenendo conto di considerazioni come leggibilità, efficienza e manutenibilità del codice. La discussione e il confronto di diversi approcci possono portare a una migliore comprensione dell’algoritmo e delle sue implementazioni in Python, perciò scrivete nei commenti sotto e dite la vostra!

Esplora il mondo della programmazione con il libro “50 Algoritmi per imparare Python” e libera la tua creatività!