Sviluppiamo un algoritmo con Algobuild che calcoli se due numeri sono amicabili.
Definizione di numeri amicabili
Due numeri in matematica si dicono amicabili o amicali o amici se la somma dei divisori propri di uno (escluso il numero stesso) è uguale all’altro numero e viceversa.
Facciamo un esempio:
La coppia di numeri 220 e 284 sono amicabili.
Infatti i divisori di 220 sono: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110.
Se li sommiamo otteniamo il numero 284
Allo stesso modo i divisori di 284 sono: 1, 2, 4, 71, 142.
La somma di tutti i divisori fa 220.
Quindi si dice che i numeri sono amicabili.
Ci sono altri esempi di numeri amicabili, ad esempio 1184 e 1210 oppure 2620 e 2924, ecc…
Algoritmo che calcola se due numeri sono amicabili con Algobuild
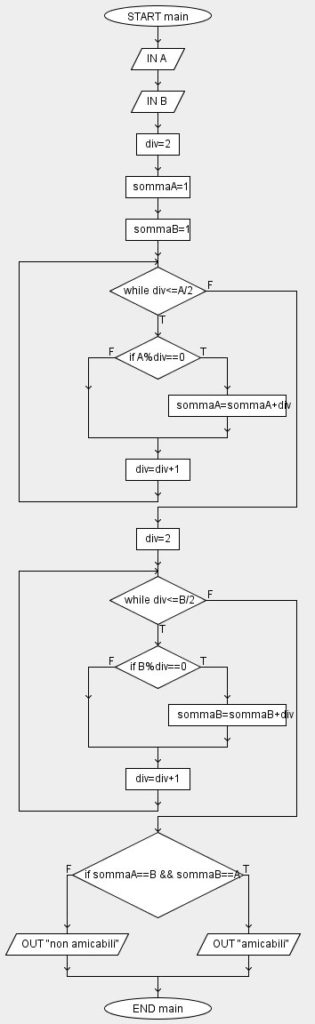
Per realizzare l’algoritmo prendiamo in input A e B, che rappresentano i due numeri presi in input su cui fare il controllo per vedere se sono amicabili.
Impostiamo una variabile div, che rappresenta i divisori, e la facciamo partire da 2.
Facciamo partire div da 2 poiché è scontato che qualsiasi numero si possa dividere per 1, pertanto faccio senza a farlo, risparmio operazioni.
Facciamo poi partire la somma dei due divisori direttamente da 1 anziché da zero.
Quindi poniamo sommaA=1 e sommaB=1.
Successivamente finché il divisore non raggiunge A/2, continuiamo a dividere A per il divisore.
Se il resto della divisione di A diviso div (A%div) è uguale a zero allora div sarà sicuramente divisore, e lo sommiamo alla sommaA; altrimenti lo ignoriamo e andiamo avanti.
In ogni caso si incrementerà il contatore div di uno.
Perché ci fermiamo ad A/2?
Perché è scontato che se dividiamo un numero per un numero superiore alla sua metà avremo sempre resto diverso da zero; ovvero sarà sempre un numero con la virgola. Quindi risparmieremo tante operazioni se ci fermiamo ad A/2.
Lo stesso procedimento possiamo ripeterlo per B, avendo cura di portare il div nuovamente a due una volta che terminiamo con A.
Alla fine confrontiamo la sommaA con B e la sommaB con A. Se entrambi i risultati sono veri allora i numeri sono amicabili, altrimenti no.
Alcuni link utili
Indice argomenti diagramma a blocchi
Divisori di un numero con algobuild
Algoritmi di selezione sugli angoli
Numeri amicabili con algobuild