Sviluppiamo l’algoritmo Merge Sort in Python, uno dei più famosi algoritmi di ordinamento che sfrutta il metodo divide et impera, così come il Quick Sort.
Innantitutto spieghiamo il funzionamento di questo algoritmo.
Dapprima suddiviamo la lista in due sottoliste e poi a mano a mano in parti ancora più piccole. Poi utilizziamo una funzione ricorsiva su ciascuna sottolista ed infine combiniamo il risultato in modo da ottenere la soluzione all’algoritmo di ordinamento.
Merge Sort Python – solution
Supponiamo di avere una lista di numeri interi:
numbers = [6,12,4,3,7,8]
Indichiamo l’indice che punta al numero 6 con p e l’indice che punta al numero 8 con r.
numbers = [p, …, …, r]
Come primo passo, dunque, dividiamo la lista a metà utilizzando un altro indice, ad esempio q:
quindi avremo numbers_1 = [p,…,…,q] e numbers_2 = [q+1,…,…,r]
Si continua a dividere finchè non può essere più diviso. Questa condizione si verifica quando l’array è vuoto oppure è rimasto solo un elemento (ovvero 0 elementi oppure 1).
Su ciascuna delle due metà, poi, si invoca la funzione di ordinamento ricorsiva. Infine si combina tutto.
Nel nostro esempio si ha:
numbers = [6,12,4,3,7,8]
da cui ne deriva: numbers_1 = [6,12,4,] e numbers_2 = [3,7,8] e così via.
Ecco, dunque, una rappresentazione grafica di quello che succede:
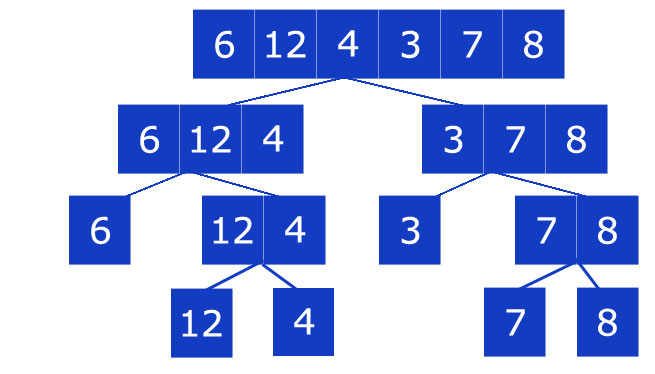
Adesso che tutti gli elementi sono divisi, utilizziamo una lista di appoggio ed iniziamo l’ordinamento.
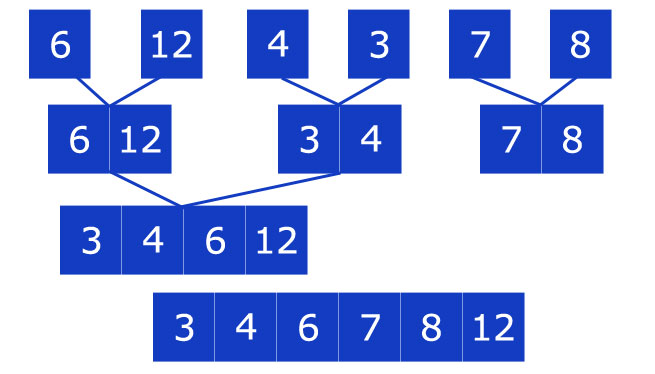
La seconda parte dell’algoritmo di Merge Sort, dunque, riguarda l’ordinamento effettivo degli elementi in un ordine che può essere crescente o decrescente.
Scegliamo un ordinamento crescente. Ordiniamo e poi combiniamo ciascuna parte delle sottoliste.
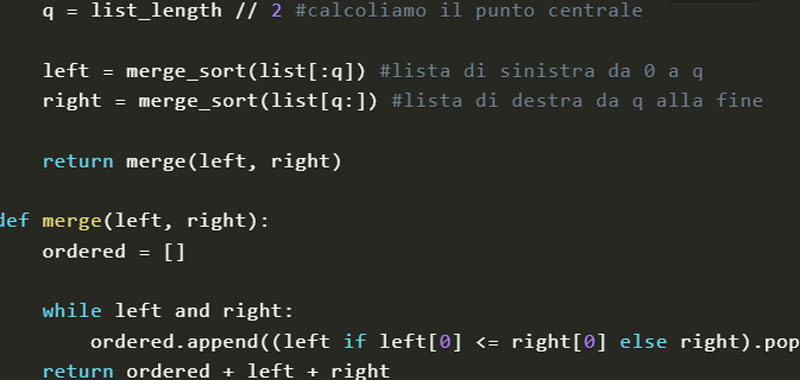
Merge Sort Python – code
Ecco dunque una possibile soluzione all’algoritmo:
def merge_sort(list):
list_length = len(list)
if list_length == 1:
return list
q = list_length // 2 #calcoliamo il punto centrale
left = merge_sort(list[:q]) #lista di sinistra da 0 a q
right = merge_sort(list[q:]) #lista di destra da q alla fine
return merge(left, right)
def merge(left, right):
ordered = []
while left and right:
ordered.append((left if left[0] <= right[0] else right).pop(0))
return ordered + left + right
numbers = [10,5,12,1,9]
print(numbers)
sorted_list = merge_sort(numbers)
print(sorted_list)
Provate il codice nel compilatore sotto:
Chiaramente quella proposta è una possibile soluzione all'algoritmo Merge Sort in Python, implementate pure la vostra e scrivetela nei commenti sotto.
Alcuni link utili
Indice tutorial sul linguaggio Python
1 – Introduzione al linguaggio Python
2 – Le variabili
3 – Operatori aritmetici e di assegnazione
4 – Stringhe
5 – Casting
6 – Input e print
8 – Errori in Python
9 – Script Python
10 – Scambio di variabili
11 – Modulo math