In this lesson we will develop the Euclidean algorithm in Python.
Euclid’s algorithm is a method used to find the greatest common divisor between two integers.
By greatest common factor, GCD, between two integers we denote the greatest common divisor of both.
Euclidean algorithm consists in dividing the two numbers and considering the remainder. The procedure ends when the remainder is found equal to zero.
Let’s take some examples.
Euclidean algorithm Python – First example
Let’s take two numbers for example 20 and 15 and proceed according to Euclid’s algorithm.
First pass: a / b i.e. 20/15 = 1 remainder 5 – the remainder is non-zero, so I keep dividing.
The second step will thus be, exchanging a with b and b with r, that is 15/5 = 3 remainder 0.
We found the remainder equal to zero, so the GCD is 5.
Euclidean algorithm Python – Second example
Let’s create a second example in order to understand how Euclid’s algorithm works.
So let’s take the numbers 64 and 30.
64/30 = 2 remainder 4 – the remainder is non-zero, so we keep dividing.
30/4 = 7 remainder 2 – the remainder is non-zero, so we keep dividing.
4/2 = 2 remainder 0
The remainder is zero, so the GCD is 2.
Euclidean algorithm in Python
Let’s now implement this algorithm in Python.
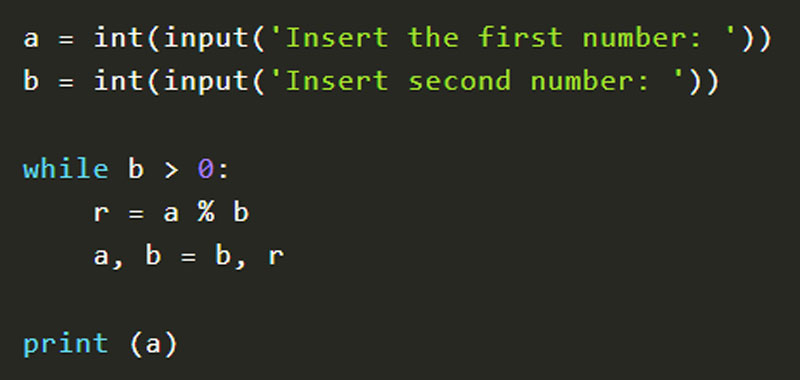
First of all we take as input the two numbers a and b. Then as long as b is greater than 0, we calculate the remainder of the divison of a divided by b and exchange a with b and b with r. So let’s print a.
So here is the complete code that represents the Euclidean algorithm in Python:
a = int(input('Insert the first number: '))
b = int(input('Insert the second number: '))
while b > 0:
r = a % b
a, b = b, r
print (a)
You can also test the code in the online Python compiler in that link: Python compiler online.
This is a possible implementation of the Euclidean algorithm, in the next lesson we will do other examples on loops in Python.
Some useful links
How to find the maximum of N numbers