Il crivello di Eratostene è un algoritmo, piuttosto antico, per il calcolo dei numeri primi. L’ideatore del crivello è stato il matematico Eratostene di Cirene da cui appunto deriva il nome.
Essendo un metodo piuttosto semplice, viene spesso implementato in molti linguaggi di programmazione a scopo didattico.
In questa lezione proponiamo il crivello di Eratostene in linguaggio C, sviluppato con le funzioni e gli array.
Metodo del crivello di Eratostene
Il metodo per trovare i numeri primi consiste nello scrivere i numeri naturali da 2 fino ad n. Dopo si cancellano tutti i multipli del primo numero, poi quelli del secondo e così via.
Facciamo un esempio con n=20. Avremo:
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Iniziamo cancellando tutti i multipli di 2, evidenziandoli di rosso:
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Quindi ecco i numeri rimasti:
2, 3, 5, 7, 9, 11, 13, 15, 17, 19
Adesso prendiamo il numero successivo alla lista che è il numero 3 e togliamo quindi tutti i multipli di 3:
2, 3, 5, 7, 9, 11, 13, 15, 17, 19
E così via, ma non essendoci più multipli, i numeri restanti sono:
2, 3, 5, 7, 11, 13, 17, 19
Quindi ecco i numeri primi da 2 a 20.
Sviluppo del crivello di Eratostene in linguaggio C
Implementiamo il crivello con un programma in C. Vi presento sotto il listato e poi vi spiego l’algoritmo passo passo.
Ecco dunque il listato completo del crivello di Eratostene:
#include <stdio.h>
#define N 1000
int insert(int *v) {
int i, n;
printf("Quanti numeri n: ");
scanf("%d", &n);
/*generiamo un vettore con tutti i numeri 0 dove l'indice i va da 2 ad n*/
for(i=2; i<=n; i++)
v[i]=0;
return n;
}
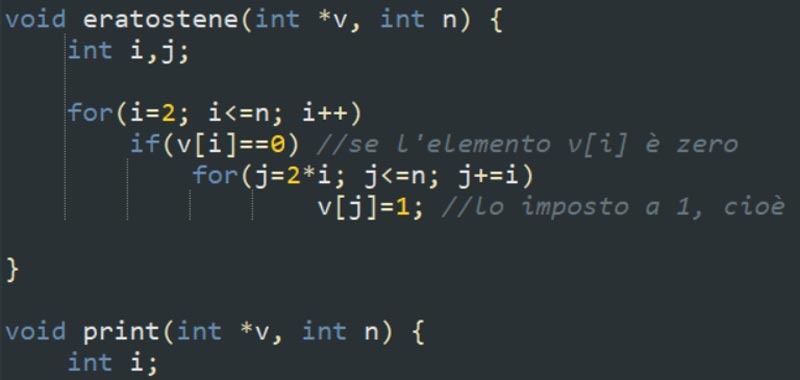
void eratostene(int *v, int n) {
int i,j;
for(i=2; i<=n; i++)
if(v[i]==0) //se l'elemento v[i] è zero
for(j=2*i; j<=n; j+=i)
//imposto v[j] a 1, cioè escludo i suoi multipli
v[j]=1;
}
void print(int *v, int n) {
int i;
for(i=2; i<=n; i++)
if(v[i]==0) //se il numero è primo
printf("%d\t",i); //stampo i risultati
}
int main() {
int a[N],n;
n=insert(a);
eratostene(a,n);
print(a,n);
return 0;
}
Per implementare l’algoritmo del crivello di Eratostene quindi faremo uso dei vettori e delle funzioni (potevo anche farne a meno, ma volevo consolidarne l’uso).
Quindi chiediamo quanto deve essere n, ovvero fino a quale numero calcolare i numeri primi e con un ciclo for inizializziamo l’array con tutti i numeri 0.
L’array avrà l’indice che va da 2 a n.
Adesso dobbiamo trovare i numeri primi e per farlo prendiamo in considerazione il primo numero con indice 2. Controlliamo se ci sono multipli di 2 e se vero settiamo l’elemento a 1.
Agiamo dunque così:
for(i=2; i<=n; i++) i=2
if(v[i]==0) vero
for(j=2*i; j<=n; j+=i) j=4
v[j]=1; v[4]=1;
j=j+i cioè j=4+2=6
dato che j<=n, cioè 4<=20 è vera, continuiamo il ciclo interno.
for(j=2*i; j<=n; j+=i) j=6
v[j]=1; v[6]=1;
dato che j<=n, cioè 6<=20 è vera, continuiamo il ciclo interno.
j=j+i cioè j=6+2=8
procediamo analogamente per gli altri numeri e quindi: v[8]=1, v[10]=1, v[12]=1, v[14]=1, v[16]=1, v[18]=1, v[20]=1 in questo caso avremo che il passo successivo è j=j+2, cioè j=22 e la condizione j<=n non è più verificata. Pertanto si procede ad incrementare i dal ciclo più esterno.
Adesso dunque i=3
for(i=2; i<=n; i++) i=3
if(v[i]==0) vero
for(j=2*i; j<=n; j+=i) j=6
v[j]=1; v[6]=1; //in realtà già era stata calcolato
j=j+i cioè j=6+3=9
dato che j<=n, cioè 9<=20 è vera continuiamo il ciclo interno.
for(j=2*i; j<=n; j+=i) j=9
v[j]=1; v[9]=1;
dato che j<=n, cioè 9<=20 è vera continuiamo il ciclo interno.
j=j+i cioè j=9+3=12
procediamo analogamente per gli altri numeri e quindi: v[12]=1, v[15]=1, v[18]=1 in questo caso avremo che il passo successivo è j=j+3, cioè j=21 e la condizione j<=n non è più verificata. Pertanto si procede ad incrementare i dal ciclo più esterno.
Si procede dunque con i=4 ma in questo caso if(v[i]==0) risulta falsa in quanto avevamo impostato v[4]=1; quindi si incrementa nuovamente i che diventa 5 e si procede con lo stesso ragionamento di prima.
Al termine quelli rimasti sono i numeri primi e li stampiamo semplicemente con queste istruzioni:
for(i=2; i<=n; i++)
if(v[i]==0) //se il numero è primo
printf(“%d\t”,i); //stampo i risultati
Cioè scorriamo tutto l’array, se l’elemento contenuto in esso è zero, vuol dire che il numero è primo, dunque stampo l’indice.
Notiamo anche che, se volessimo invece stampare tutti i numeri non primi, basterebbe impostare:
for(i=2; i<=n; i++)
if(v[i]==1) //se il numero non è primo
printf("%d\t",i); //stampo i risultatiQuesto è solo un possibile esempio di come impostare l’algoritmo che rappresenta il calcolo dei numeri primi con il crivello di Eratostene.
Alcuni link utili
Realizzare un menù di scelta in C
Somma elementi diagonale principale di una matrice
Come sommare gli elementi della cornice esterna
Ricerca elementi in una matrice
Quali metodi per inserire dati in una matrice