Algoritmo di Euclide, calcolo del massimo comune divisore

L’algoritmo di Euclide è un metodo per trovare il massimo comune divisore tra due numeri interi.

Ricordiamo che il massimo comune divisore, MCD, tra due numeri interi è il più grande divisore comune ad entrambi.

Come si determina? Si calcola per ognuno l’elenco dei divisori e tra i due gruppi si individua il numero più grande.

Ricordo che vi avevo presentato l’algoritmo in questa lezione: massimo comune divisore con scratch.

Ma Euclide riuscì a risolvere il problema senza calcolare tutti i divisori!

L’idea è stata questa: anziché calcolare il MCD tra i due numeri a e b, si divide a per b e si calcola il resto r.

Dopo si ricava il MCD tra b ed r e si procede fino a quando si ha resto 0. L’ultimo divisore è il MCD cercato.

Facciamo un esempio:

Prendiamo i due numeri 40 e 15 e procediamo secondo l’algoritmo di Euclide.

Primo passaggio: a/b cioè 40/15=2 resto 10

Secondo passaggio scambiamo a con b e b con r cioè 15/10=1 resto 5

Terzo passaggio scambiamo a con b e b con r cioè 10/5=2 resto 0.

Abbiamo trovato resto zero, quindi il MCD è 5.

Facciamo ancora un altro esempio:

Consideriamo i due numeri 84 e 48.

Avremo questi passaggi:

84/48=1 resto 36

48/36=1 resto 12

36/12=3 resto 0

Allora MCD è 12.

Algoritmo di Euclide per il MCD con Scratch

Bene una volta capito il procedimento sviluppiamo l’algoritmo di Euclide con Scratch.

Innanzitutto scegliamo uno sfondo e uno sprite qualsiasi.

Dopo creiamo le variabili necessarie:

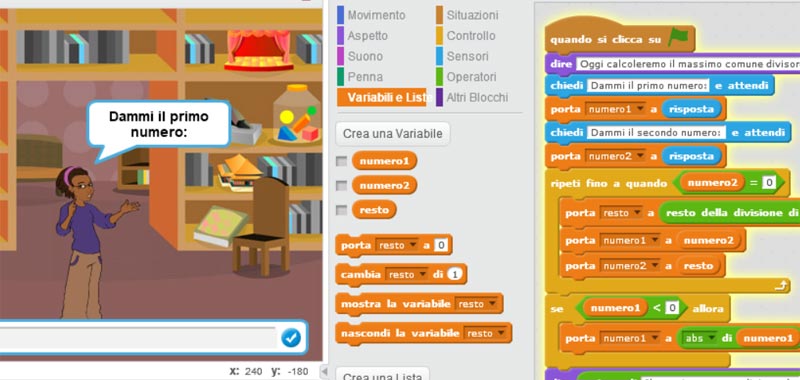
Poi realizziamo il nostro codice a blocchi.

– Prendiamo inizialmente i nostri due numeri in input.

– Dopo finché il secondo numero non diventa zero facciamo queste operazioni:

– Memorizziamo nella variabile resto il resto della divisione di numero1 per numero2.

– Nella variabile numero1 memorizziamo il valore di numero2 e nella variabile numero2 memorizziamo il resto.

Provando con l’esempio sopra:

numero1=84 e numero2=48

quindi resto=numero1%numero2 cioè resto=84%48 ovvero resto=36.

Poi memorizziamo in numero1 il valore di numero2 e in numero2 il valore di resto e quindi numero1=48 e numero2=36.

E così via, faccio questi passaggi finché non ottengo più il resto.

Notate che dopo il ciclo ho inserito un’istruzione condizionale: se il numero1 che corrisponde al nostro massimo comune divisore è negativo allora diventa positivo. Perché ad esempio il MCD(84,48)=MCD(-84,48)=MCD(84, -48)=MCD(-84, -48).

Ecco il diagramma a blocchi completo.

Chiaramente si poteva introdurre il controllo per verificare che i numeri presi in input siano interi. Provate a farlo, vi darò la soluzione in un prossimo articolo.

Come si nota l’algoritmo di Euclide per il massimo comune divisore è una soluzione molto più semplice rispetto alla precedente.